[How to] Comment tracer des flèches sur une carte avec Tableau ?

Introduction
Je n’aime pas écrire des intros. Personne ne les lit de toute façon. Laissez-moi simplement dire qu’aujourd’hui, je vais vous montrer l’une des façons de tracer des flèches sur une carte que j’ai utilisée pour l’un de mes projets personnels, et qui peut vous être utile à vous aussi. À la fin de ce tutoriel, vous serez en mesure de réaliser des cartes comme celle-ci :
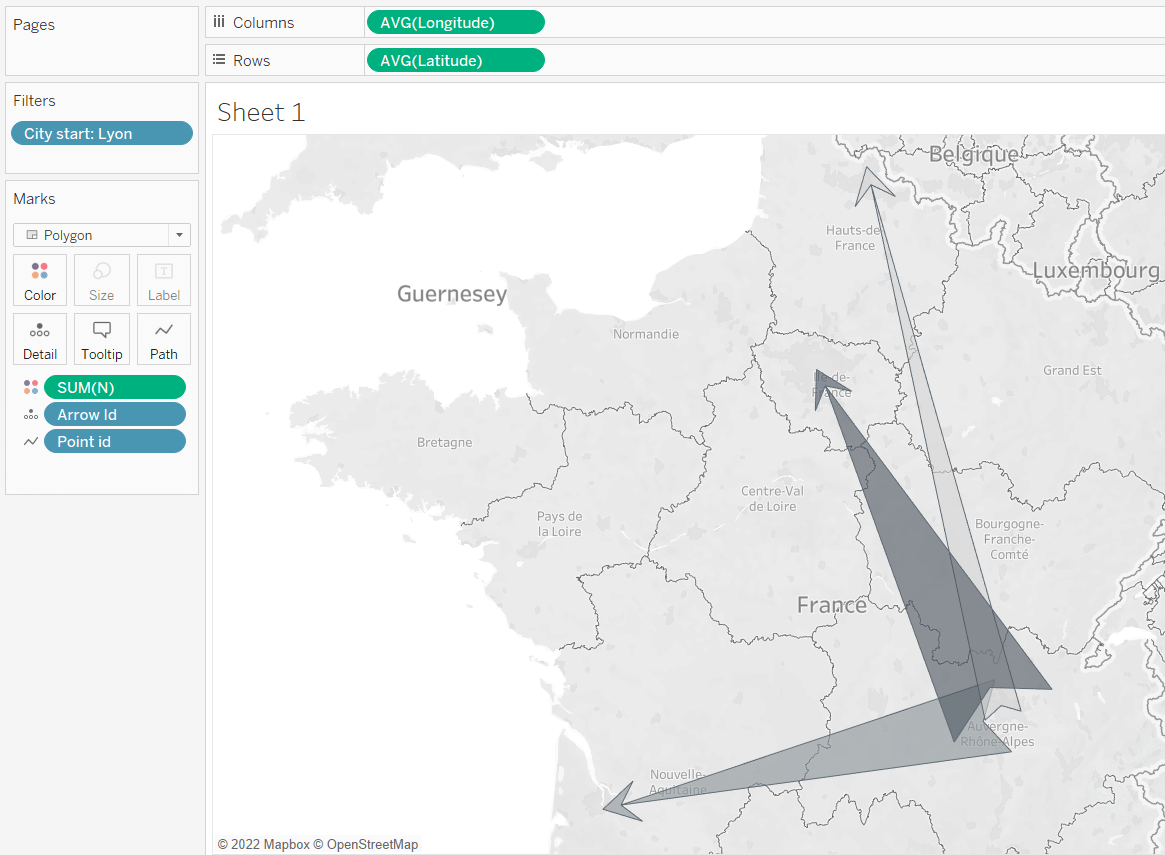
Parlons d’abord de ce que nous allons faire et de la logique derrière. Car si vous comprenez que vous pouvez personnaliser vos flèches à votre goût (oui, je ne vais pas prétendre que mes flèches sont les plus belles, bien qu’elles le soient très certainement).
1. Les polygones !
Les polygones requièrent des ensembles ordonnés et fermés de coordonnées X, Y. Cela signifie que
- Chaque flèche aura son propre identifiant unique
- Chaque point de chaque flèche aura son propre identifiant unique.
- Ces identifiants indiquera dans quel ordre la ligne sera tracée à travers ces points.
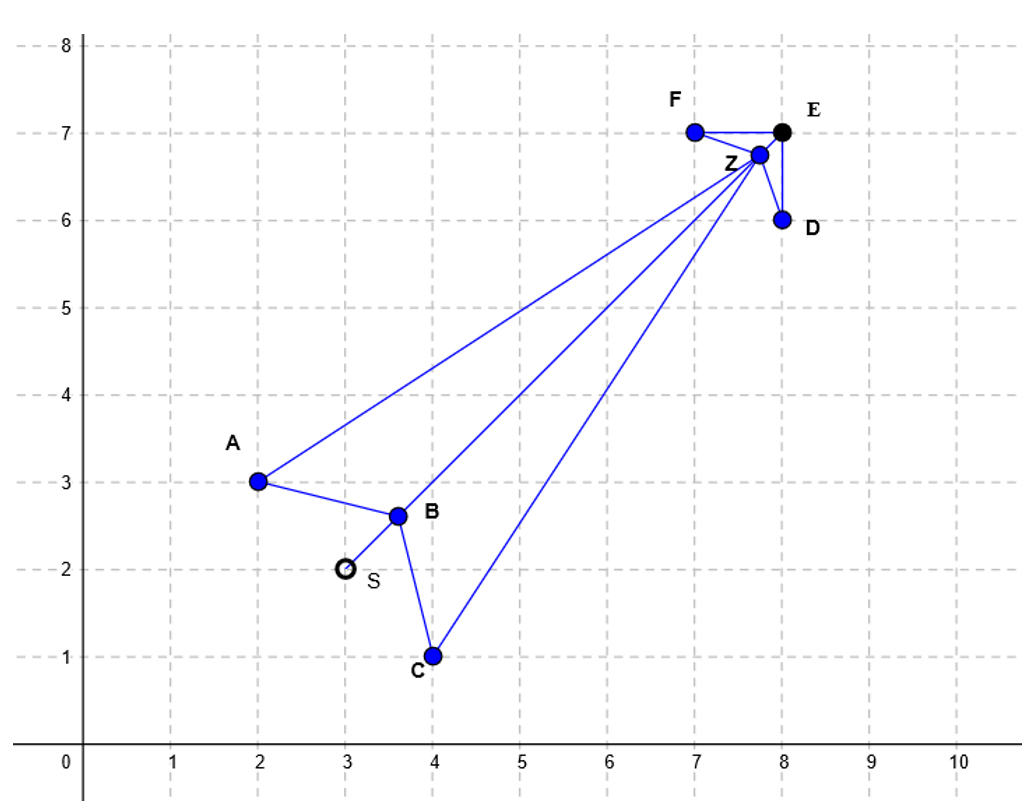
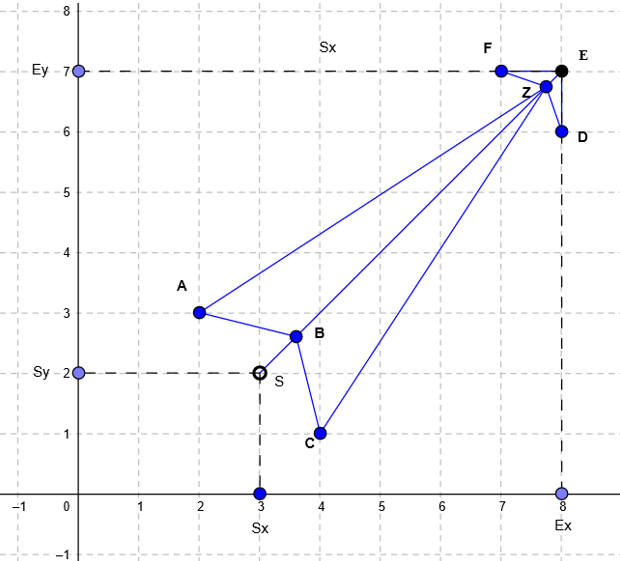
Et voici notre squelette de flèche.
Ici, vous pouvez voir les 8 points (l’ordre compte!): A, B, C, Z, D, E, F, Z.
Vous avez peut-être remarqué que nous avons deux Z ici : pour ce type de flèche, vous devez avoir une valeur deux fois, sinon vos points ne seront pas connectés correctement. Le dernier point sera automatiquement relié au premier. Ici, E est le point final et S est le point de départ de notre ensemble de données.
Nous aurons besoin de la structure des données sources suivante :
| Identifiant flèche | Identifiant point | X | Y |
| 1 | 1 | (A1x coordinate) | (A1y coordinate) |
| 1 | 2 | (B1x coordinate) | (B1y coordinate) |
| 1 | 3 | (C1x coordinate) | (C1y coordinate) |
| 1 | 4 | (Z1x coordinate) | (Z1y coordinate) |
| 1 | 5 | (D1x coordinate) | (D1y coordinate) |
| 1 | 6 | (E1x coordinate) | (E1y coordinate) |
| 1 | 7 | (F1x coordinate) | (F1y coordinate) |
| 1 | 8 | (Z1x coordinate) | (Z1y coordinate) |
| 2 | 1 | (A2x coordinate) | (A2y coordinate) |
| 2 | 2 | (B2x coordinate) | (B2y coordinate) |
Nous allons placer la longitude dans les colonnes, la latitude dans les lignes, choisir le polygone comme type de graphique, glisser et déposer l’identifiant de la flèche dans le détail et l’identifiant du point dans le chemin.
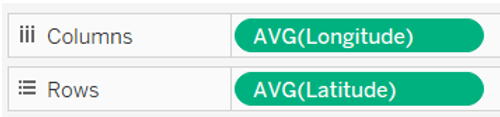
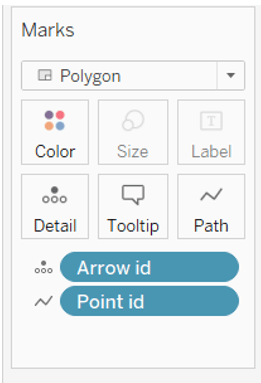
2. Trigonométrie :
Pour calculer les coordonnées, nous utiliserons le théorème de Pythagore et la formule trigonométrique suivante :
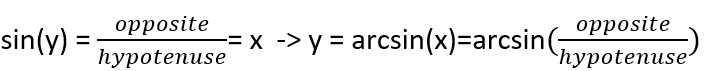
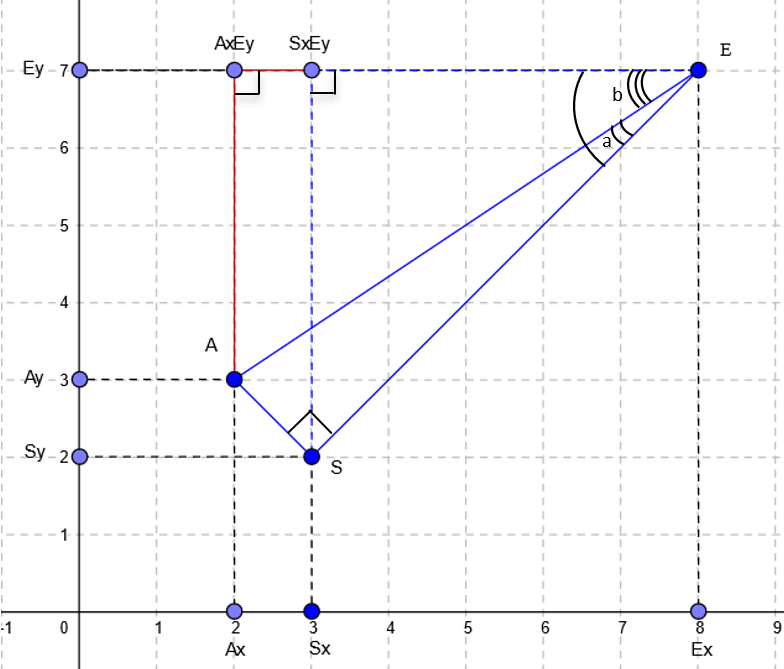
Sur l’exemple du point A, je vais vous montrer comment trouver toutes les coordonnées, en connaissant les coordonnées du point S (point de départ) et du point E (point d’arrivée) ainsi que la longueur souhaitée de AS (n).
Nous pouvons calculer Ex-Sx et Ey-Sy puisque nous connaissons toutes les coordonnées nécessaires. Grâce à cela, nous pouvons également calculer la longueur de ES et AE :
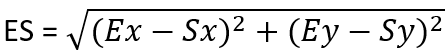
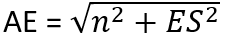
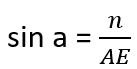
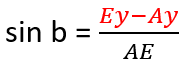
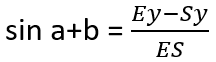
We can find Ey-Ay and Ex-Ax:
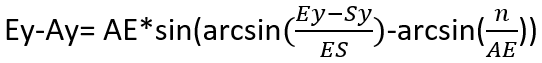
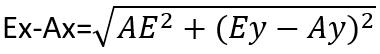
Pour trouver Ax, il suffit alors de soustraire la valeur de Ex-Ax de la valeur de Ex. La même logique s’applique à Ay :
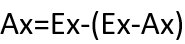
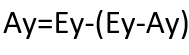
Si vous voulez personnaliser votre flèche, il suffit de la tracer différemment sur votre toile et de calculer les coordonnées en utilisant la même logique.
3. Longitude-latitude -> X-Y
- Il est également important de comprendre que la longitude-latitude ne peut pas être utilisée telle quelle pour les calculs en 2D. Nous devons d’abord les transformer en coordonnées X-Y, puis effectuer tous les calculs pour trouver les coordonnées X-Y de tous les points et enfin les transformer en valeurs de longitude-latitude.
Cet article explique la logique des calculs que j’ai utilisés dans mon classeur.
Voici les formules que nous allons utiliser :
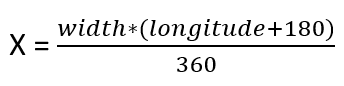
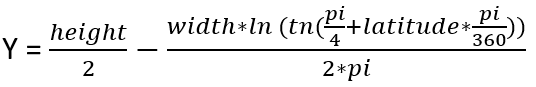
And reversed:
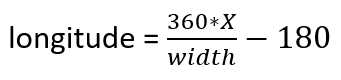
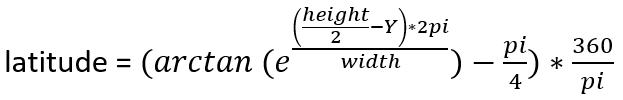
J’ai utilisé 1440 pixels comme valeur de largeur et 720 pixels comme valeur de hauteur. Je crois que le choix n’a pas vraiment d’importance puisque nous allons reconvertir les coordonnées en valeurs de longitude-latitude.
Création d’un ensemble de données
Maintenant, il est temps de commencer. Je vais prendre la longitude-latitude de 4 villes françaises et créer des flèches entre elles.
| Ville | Latitude | Longitude |
| Paris | 48.85499357107459 | 2.3346734272193794 |
| Lille | 50.62374591673762 | 3.0110800296755196 |
| Lyon | 45.68554335428289 | 4.853667452230858 |
| Bordeaux | 44.79603794403178 | -0.547927769672152 |
Pour ce faire, je crée dans mon ensemble de données toutes les paires possibles de ces villes. Pour chaque paire, je vais également définir un n choisi au hasard, qui définira l’épaisseur des flèches. Voici ce que j’ai obtenu :
| Départ de ville | Latitude de début | Longitude de début | Fin de ville | Latitude de fin | Longitude de fin | n | ID flèche | 0 |
| Paris | 48.85499357107459 | 2.3346734272193794 | Lille | 50.62374591673762 | 3.0110800296755196 | 3 | 1 | 0 |
| Paris | 48.85499357107459 | 2.3346734272193794 | Lyon | 45.68554335428289 | 4.853667452230858 | 2 | 2 | 0 |
| Paris | 48.85499357107459 | 2.3346734272193794 | Bordeaux | 44.79603794403178 | -0.547927769672152 | 1 | 3 | 0 |
| Lille | 50.62374591673762 | 3.0110800296755196 | Paris | 48.85499357107459 | 2.3346734272193794 | 3 | 4 | 0 |
| Lille | 50.62374591673762 | 3.0110800296755196 | Lyon | 45.68554335428289 | 4.853667452230858 | 2 | 5 | 0 |
| Lille | 50.62374591673762 | 3.0110800296755196 | Bordeaux | 44.79603794403178 | -0.547927769672152 | 2 | 6 | 0 |
| Lyon | 45.68554335428289 | 4.853667452230858 | Paris | 48.85499357107459 | 2.3346734272193794 | 3 | 7 | 0 |
| Lyon | 45.68554335428289 | 4.853667452230858 | Lille | 50.62374591673762 | 3.0110800296755196 | 1 | 8 | 0 |
| Lyon | 45.68554335428289 | 4.853667452230858 | Bordeaux | 44.79603794403178 | -0.547927769672152 | 2 | 9 | 0 |
| Bordeaux | 44.79603794403178 | -0.547927769672152 | Paris | 48.85499357107459 | 2.3346734272193794 | 3 | 10 | 0 |
| Bordeaux | 44.79603794403178 | -0.547927769672152 | Lille | 50.62374591673762 | 3.0110800296755196 | 1 | 11 | 0 |
| Bordeaux | 44.79603794403178 | -0.547927769672152 | Lyon | 45.68554335428289 | 4.853667452230858 | 2 | 12 | 0 |
ID flèche est un numéro unique par paire ville début – ville fin. La colonne 0 sera utilisée pour créer un produit cartésien avec la deuxième table. N’oubliez pas que nous devons avoir 8 lignes par ligne pour tracer nos 8 points.
La deuxième table ressemble à cela:
| 0 | Identifiant du point |
| 0 | 1 |
| 0 | 2 |
| 0 | 3 |
| 0 | 4 |
| 0 | 5 |
| 0 | 6 |
| 0 | 7 |
| 0 | 8 |
Tout d’abord, nous devons créer une source de données. 12*8 nous donnes 96 lignes:
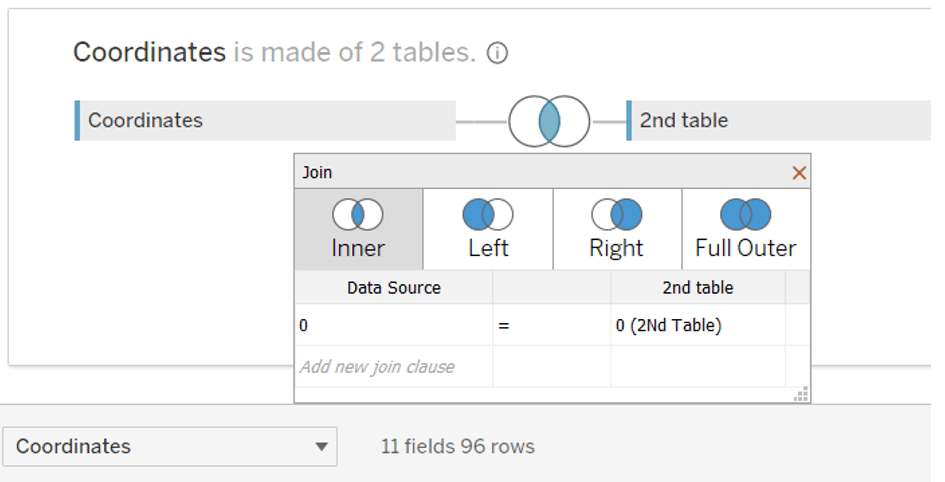
Après ça, vous pouvez cacher les deux colonnes 0, nous n’en aurons pas besoin :
Les calculs
Comme j’ai choisi 1440 pixels comme valeur de largeur et 720 pixels comme valeur de hauteur, nous pouvons déjà mettre ces valeurs dans nos formules :
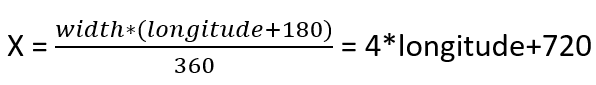
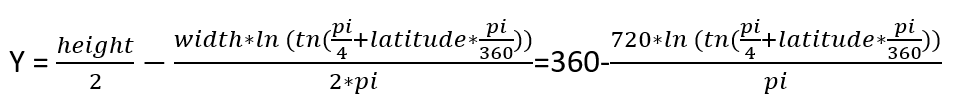
Maintenant, nous avons tout pour calculer les coordonnées X-Y pour les points S et E :
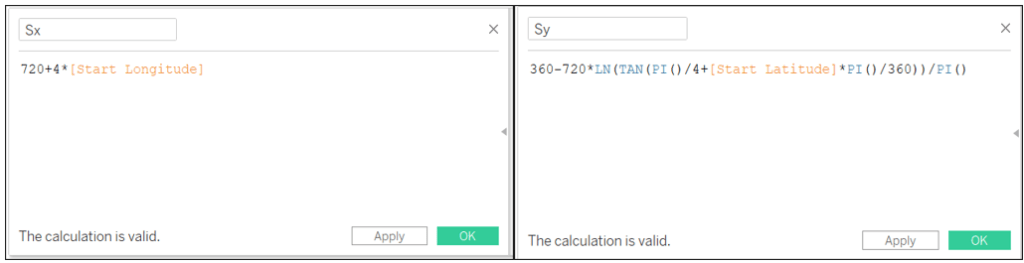
Sx: 720+4*[Longitude de départ]
Sy: 360-720*LN(TAN(PI()/4+[Latitude de départ]*PI()/360))/PI()
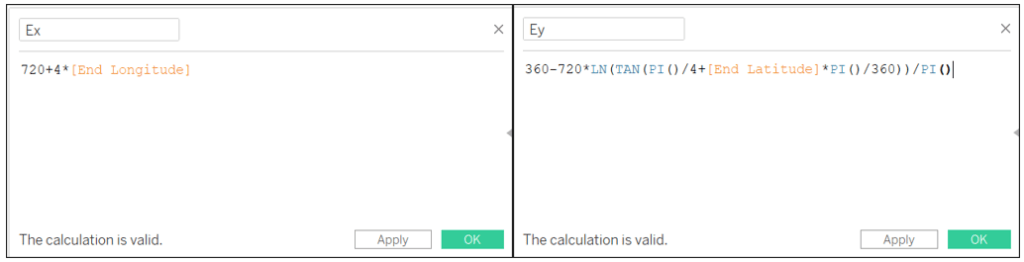
Ex: 720+4*[Longitude de fin]
Ey: 360-720*LN(TAN(PI()/4+[Latitude de fin]*PI()/360))/PI()
La prochaine étape sera de calculer les distances entre Sx et Ex, Sy etEy, entre S et E et A(C) et E.
Nous utilisons l’ABS car notre flèche peut regarder dans n’importe quelle direction et nous voulons calculer la distance entre les points qui ne peut pas être négative.
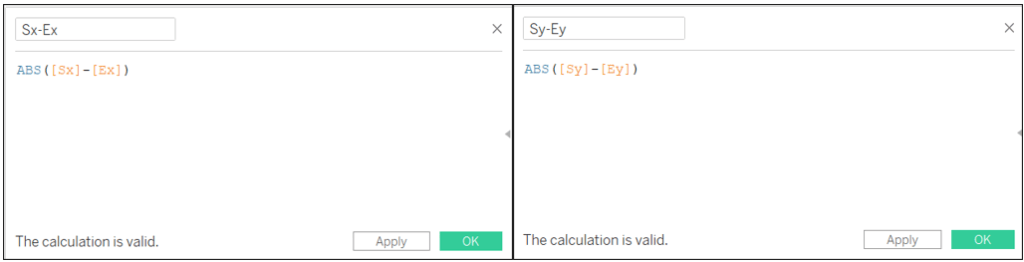
Sx-Ex: ABS([Sx]-[Ex])
Sy-Ey: ABS([Sy]-[Ey])
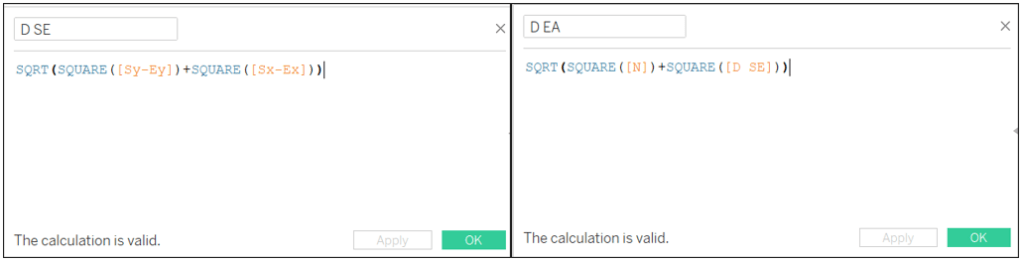
D SE: SQRT(SQUARE([Sy-Ey])+SQUARE([Sx-Ex]))
D EA: SQRT(SQUARE([N])+SQUARE([D SE]))
Maintenant, nous pouvons commencer à créer nos points. Nous commençons par le point A. D’abord, nous calculons les distances Ax-Ey et Ax-Ex :
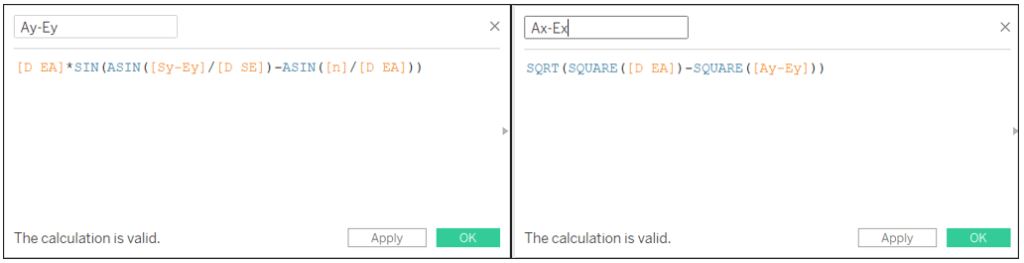
Ay-Ey: [D EA]*SIN(ASIN([Sy-Ey]/[D SE])-ASIN([N]/[D EA]))
Ax-Ex: SQRT(SQUARE([D EA])-SQUARE([Ay-Ey]))
Ensuite, en fonction de la position du point final par rapport au point de départ, nous ajouterons ou soustrairons la valeur de la distance aux coordonnées du point final :
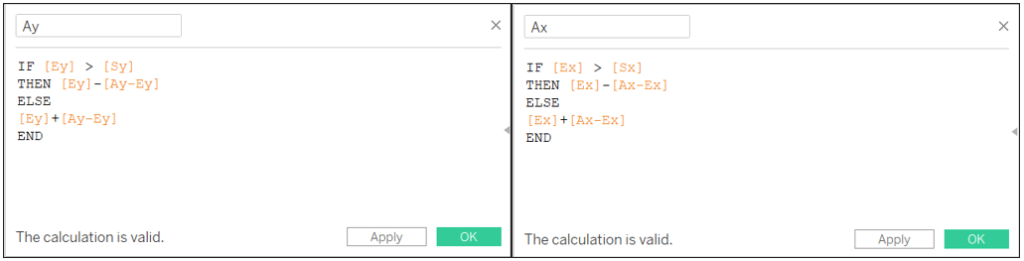
Ay: IF [Ey] > [Sy] THEN [Ey]-[Ay-Ey] ELSE [Ey]+[Ay-Ey] END
Ax: IF [Ex] > [Sx] THEN [Ex]-[Ax-Ex] ELSE [Ex]+[Ax-Ex] END
Nous faisons le même procédé pour les autres points.
Cx-Ex: [D EA]*SIN(ASIN([Sx-Ex]/[D SE])-ASIN([N]/[D EA]))
Cy-Ey: SQRT(SQUARE([D EA])-SQUARE([Cx-Ex]))
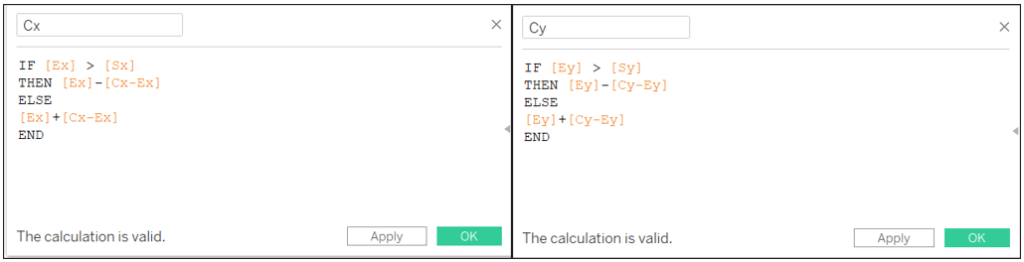
Cx: IF [Ex] > [Sx] THEN [Ex]-[Cx-Ex] ELSE [Ex]+[Cx-Ex] END
Cy: IF [Ey] > [Sy] THEN [Ey]-[Cy-Ey] ELSE [Ey]+[Cy-Ey] END
Pour le point B, j’ai défini SB = n/2. Pour le calculer j’utilise la distance entre Sy et Ay
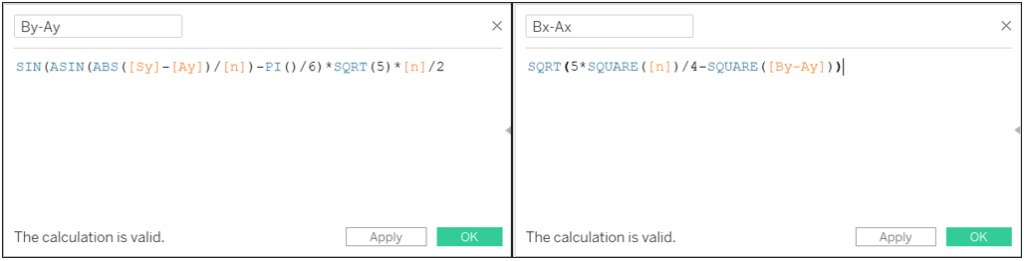
By-Ay: SIN(ASIN(ABS([Sy]-[Ay])/[N])-PI()/6)*SQRT(5)*[N]/2
Bx-Ax: SQRT(5*SQUARE([N])/4-SQUARE([By-Ay]))
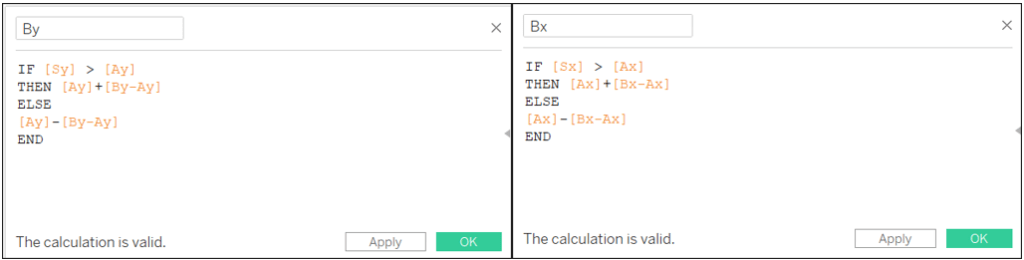
By: IF [Sy] > [Ay] THEN [Ay]+[By-Ay] ELSE [Ay]-[By-Ay] END
Bx: IF [Sx] > [Ax] THEN [Ax]+[Bx-Ax] ELSE [Ax]-[Bx-Ax] END
J’ai fait dépendre le point Z d’une constante m. My m=1
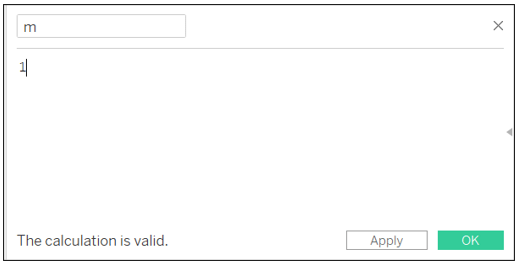
On calcule les coordonnées de Z en utilisant la proportion D SE/m :
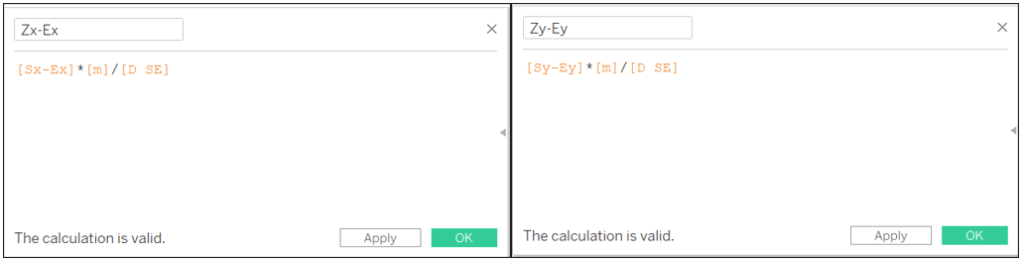
Zx-Ex: [Sx-Ex]*[m]/[D SE]
Zy-Ey: [Sy-Ey]*[m]/[D SE]
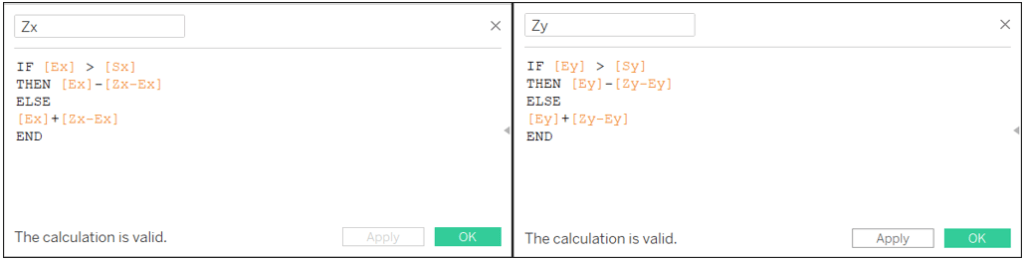
Zx: IF [Ex] > [Sx] THEN [Ex]-[Zx-Ex] ELSE [Ex]+[Zx-Ex] END
Zy: IF [Ey] > [Sy] THEN [Ey]-[Zy-Ey] ELSE [Ey]+[Zy-Ey] END
Nous avons les points D et F nous manquant.
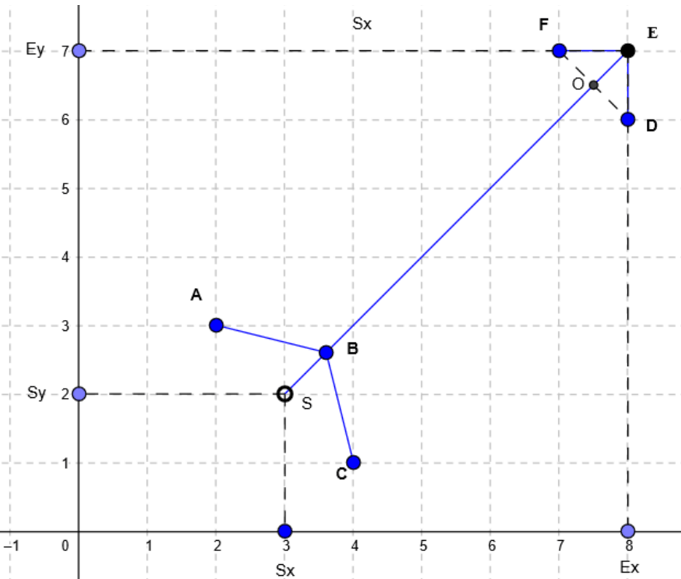
En les reliant, on obtient le point O à l’intersection avec la ligne SE. J’ai défini FO=OD=m=OE/2
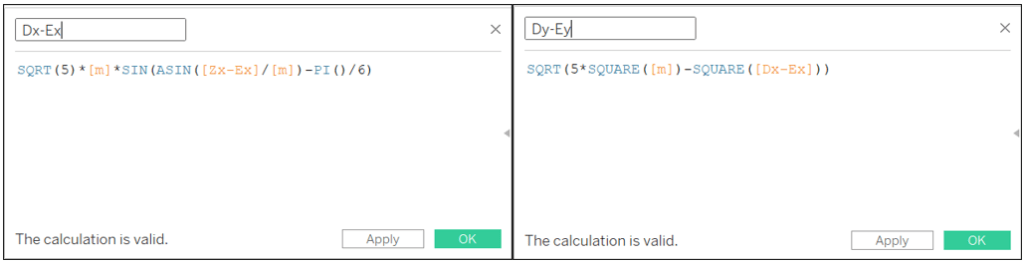
Dx-Ex: SQRT(5)*[m]*SIN(ASIN([Zx-Ex]/[m])-PI()/6)
Dy-Ey: SQRT(5*SQUARE([m])-SQUARE([Dx-Ex]))
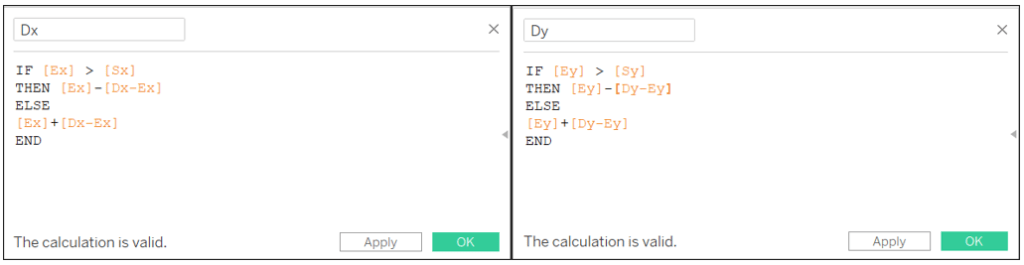
Dx: IF [Ex] > [Sx] THEN [Ex]-[Dx-Ex] ELSE [Ex]+[Dx-Ex] END
Dy: IF [Ey] > [Sy] THEN [Ey]-[Dy-Ey] ELSE [Ey]+[Dy-Ey] END
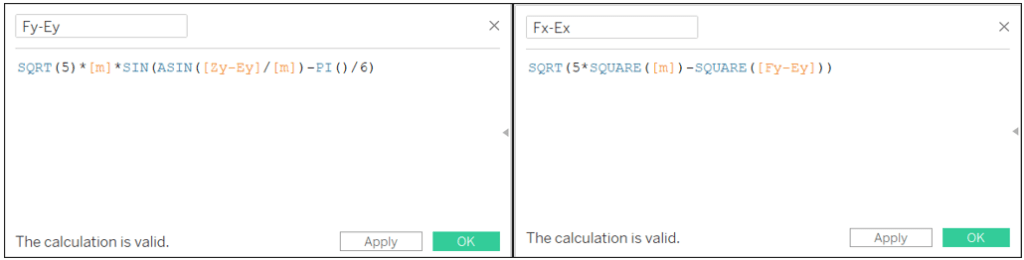
Fy-Ey: SQRT(5)*[m]*SIN(ASIN([Zy-Ey]/[m])-PI()/6)
Fx-Ex: SQRT(5*SQUARE([m])-SQUARE([Fy-Ey]))
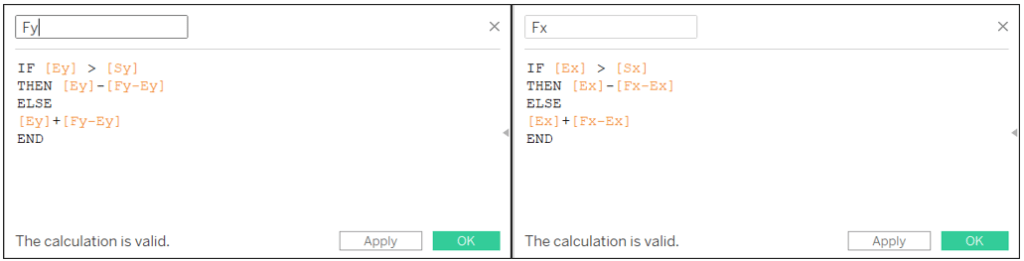
Fy: IF [Ey] > [Sy] THEN [Ey]-[Fy-Ey] ELSE [Ey]+[Fy-Ey] END
Fx: IF [Ex] > [Sx] THEN [Ex]-[Fx-Ex] ELSE [Ex]+[Fx-Ex] END
Maintenant, nous avons toutes nos coordonnées X-Y et il est temps de les convertir en valeurs de longitude et de longitude.
Comme j’ai choisi 1440 pixels comme valeur de largeur et 720 pixels comme valeur de hauteur, nous pouvons déjà mettre ces valeurs dans nos formules :
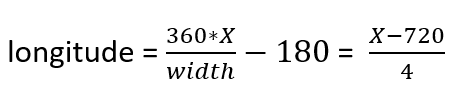
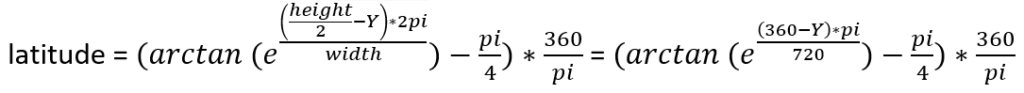
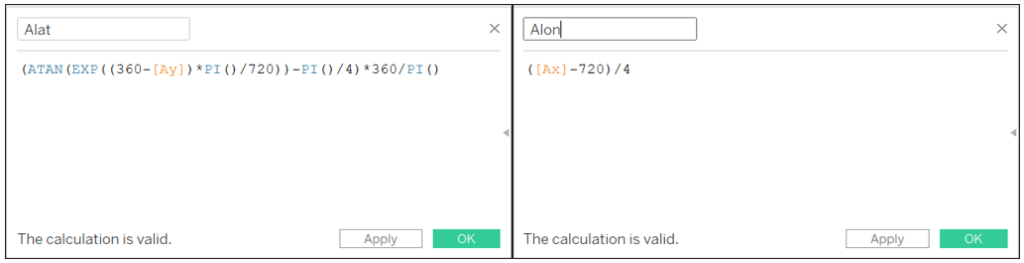
Alat: (ATAN(EXP((360-[Ay])*PI()/720))-PI()/4)*360/PI()
Alon: ([Ax]-720)/4
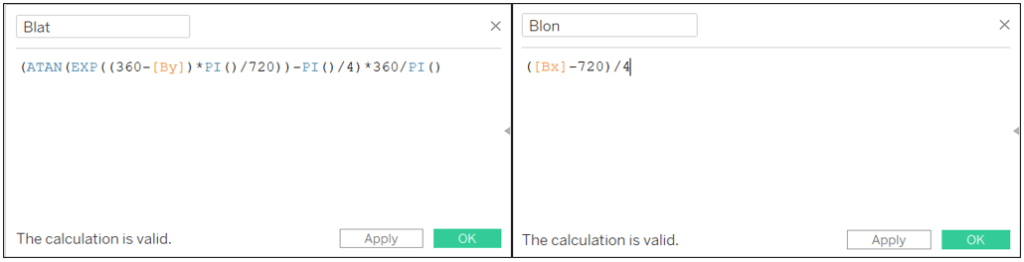
Blat: (ATAN(EXP((360-[By])*PI()/720))-PI()/4)*360/PI()
Blon: ([Bx]-720)/4
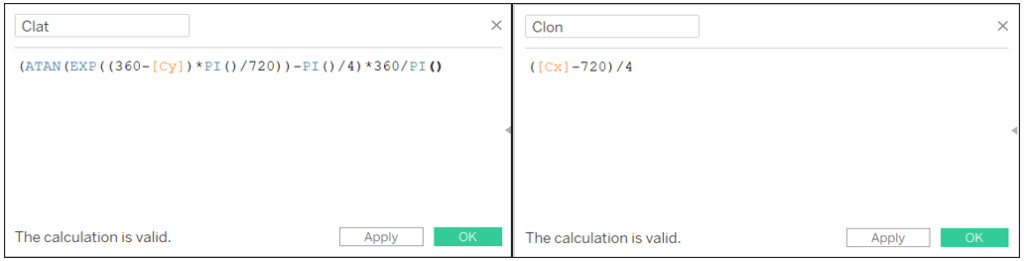
Clat: (ATAN(EXP((360-[Cy])*PI()/720))-PI()/4)*360/PI()
Clon: ([Cx]-720)/4
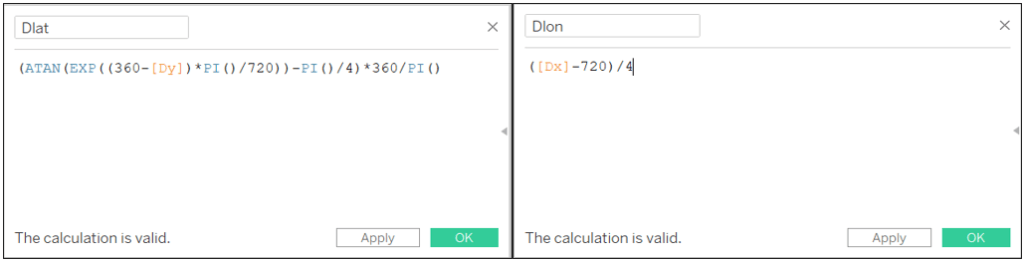
Dlat: (ATAN(EXP((360-[Dy])*PI()/720))-PI()/4)*360/PI()
Dlon: ([Dx]-720)/4
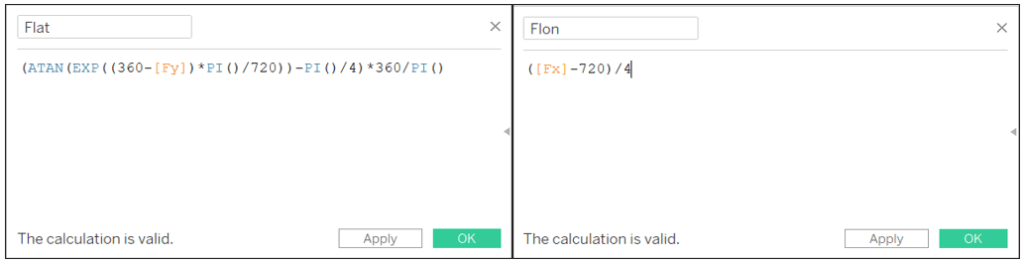
Flat: (ATAN(EXP((360-[Fy])*PI()/720))-PI()/4)*360/PI()
Flon: ([Fx]-720)/4
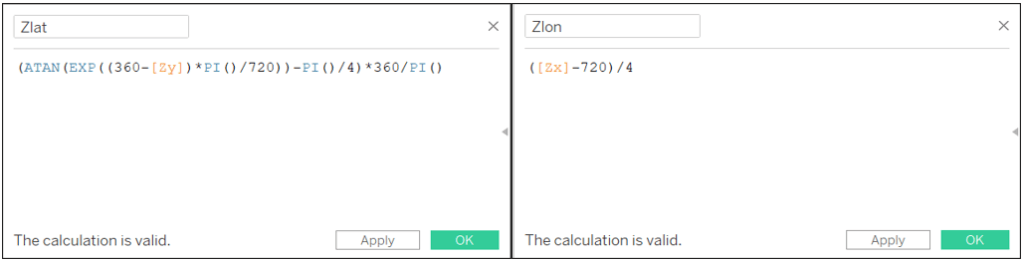
Zlat: (ATAN(EXP((360-[Zy])*PI()/720))-PI()/4)*360/PI()
Zlon: ([Zx]-720)/4
Enfin, nous devons créer des champs calculés pour collecter toutes les valeurs de longitude et de latitude dans un ordre correct.
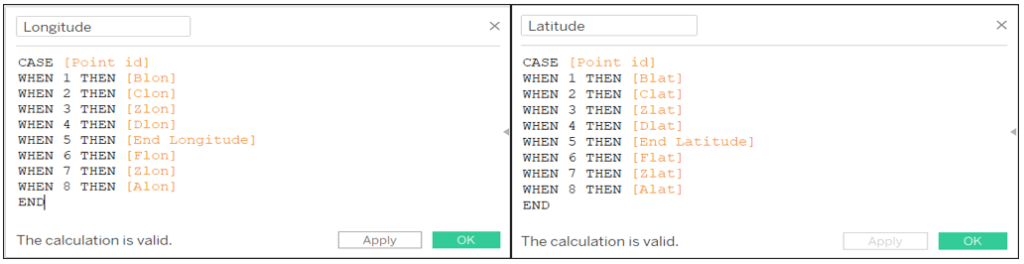
Longitude: CASE [Point id] WHEN 1 THEN [Blon] WHEN 2 THEN [Clon] WHEN 3 THEN [Zlon] WHEN 4 THEN [Dlon] WHEN 5 THEN [End Longitude] WHEN 6 THEN [Flon] WHEN 7 THEN [Zlon] WHEN 8 THEN [Alon] END
Latitude: CASE [Point id] WHEN 1 THEN [Blat] WHEN 2 THEN [Clat] WHEN 3 THEN [Zlat] WHEN 4 THEN [Dlat] WHEN 5 THEN [End Latitude] WHEN 6 THEN [Flat] WHEN 7 THEN [Zlat] WHEN 8 THEN [Alat] END
Création de flèches
Nous devons changer le rôle géographique pour les deux derniers champs calculés :
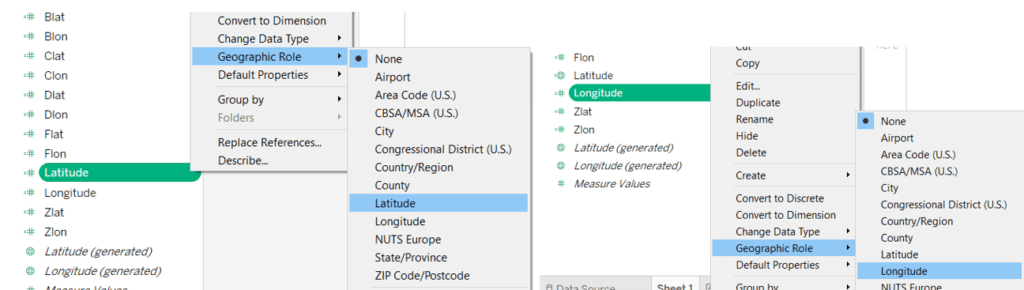
Choisissez maintenant un graphique polygonal, faites glisser et déposez la longitude dans les colonnes, la latitude dans les rangées, l’identifiant de la flèche dans le détail et l’identifiant du point dans le chemin.
Egalement, pouvez également expérimenter avec les couleurs, l’opacité, les bordures et d’autres caractéristiques pour rendre vos flèches plus belles.
Résultat:

Amusez-vous bien !
Obtenez une démo gratuite Tableau, l’outil de data visualization vous aidera à voir et comprendre vos données sur une seule plateforme facile à utiliser !

Remplissez le formulaire pour une démo gratuite !



